Since antiquity, science has studied how to elegantly cover surfaces without leaving any gaps. It turns out, the usual approach of using sharp-edged shapes to tile seamless floors, or decorating walls using mosaiced tessellations, is not nature’s first choice.
A team of mathematicians from the University of Oxford and Budapest University of Technology and Economics have discovered a new universal class of shapes called ‘soft cells’, which seem to govern natural design: found in everything from nautilus shells, a zebra’s stripes, how seeds pack into plants, to the layers of an onion. These cells have curved edges with cusp-like corners, their ends pinched together into a narrow point with an internal angle of zero degrees.
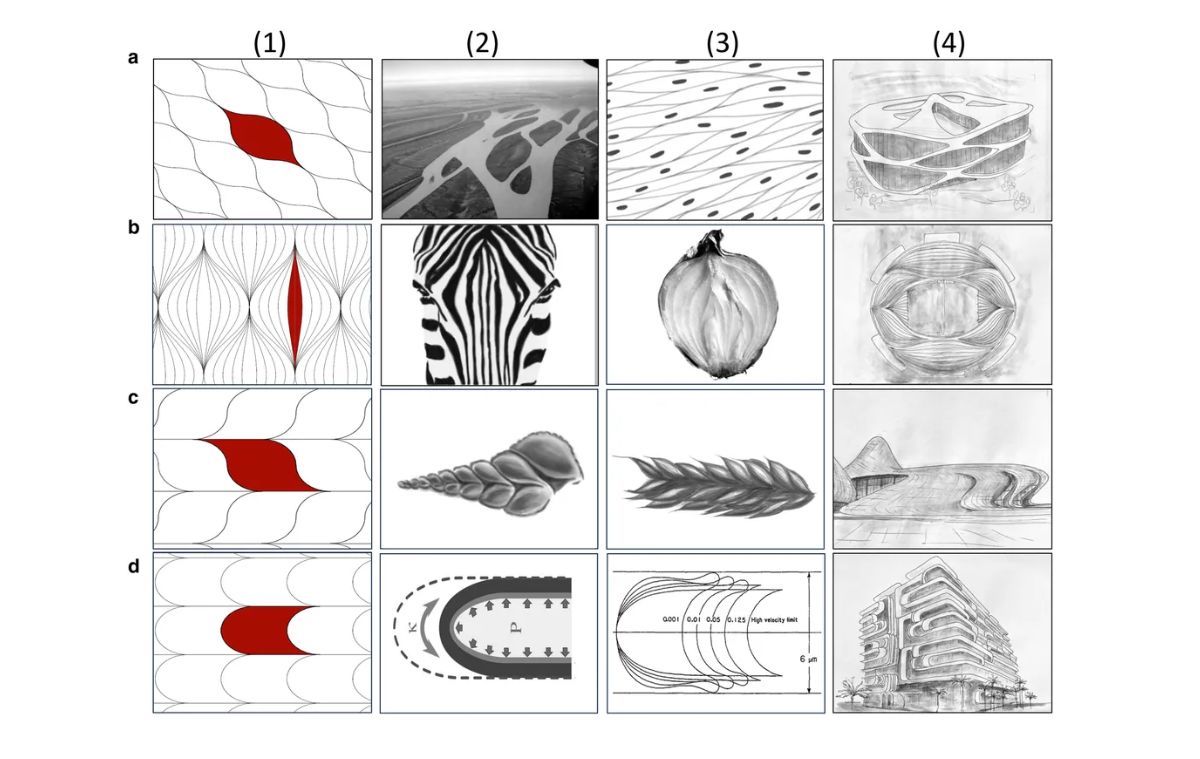Examples of soft cell types in nature and their use in architecture by Zaha Hadid. (Domokos et al./PNAS Nexus 2024/CC BY-NC 4.0)
“These shapes emerge in art, but also in biology,” the study’s lead author Professor Gábor Domokos told New Scientist. “If you look at sections of muscle tissue, you’ll see the cells having just two sharp corners, which is one less than the triangle—it is a very special kind of tiling.” The findings were published in PNAS Nexus on September 10.
Tiling is a mathematical sub-field, at its simplest exploring how polygons can cover a 2D plane without leaving gaps or overlaps. Its concepts inspire the design of packing puzzlesjigsaws, centuries of Middle Eastern weaving patterns, as well as futuristic architecture. Explorations into this realm likely started 10,000 years ago, with the advent of masonry walls.
It is on a 3D plane, however, where soft cells become more interesting. “The team first established that, in 3D, soft cells have no corners at all,” explains an Oxford statement. “Then, starting with conventional 3D tiling systems such as the cubic grid, the team showed that they can be softened by allowing the edges to bend whilst minimizing the number of sharp corners. in this process. Through doing this, they found entire new classes of soft cells with different tiling properties.”
Dongdaemun Plaza, a Seoul landmark designed using the ethos of this new shape by Zaha Hadid.
Examining the geometry of complex life, researchers found that nature seemed to “abhor sharp corners”. They also noted that architects like Zaha Hadid had ‘intuitively’ constructed soft cell-like new shapes when they wanted to avoid corners in buildings. Hadid’s topsy-turvy designs can be seen at Seoul’s Dongdaemun Plaza, the London Aquatics Center and the Heydar Aliyev Center in Baku.
Central to the study was a reliance on CT images, which showed how the inner chambers of the nautilus, a marine mollusc, is a natural example of 3D soft cells without corners. The findings seem to have been hidden in plain sightas the team’s analysis used ancient geometry that has been known for centuries.
Soft cells are why the cross section of a chambered shell shows corners, but a 3D view of the chambers do not. (Image credit: Krisztina Regõs and Lajos Czegledi)
“The universe of polygonal and polyhedral tilings is so fascinating and rich that mathematicians did not need to expand their playground,” Domokos told Natureadding that it dispels the notion that cutting-edge maths or computation is required to make remarkable findings.
Hobbyist mathematician David Smith proved this in 2023 by uncovering the ‘Einstein tile’ — a 13-sided shape that could fill an infinitely large plane without repeating its pattern. Smith, 64, was a retired printing technician who had stumbled upon it while ‘messing about with shapes’. Also known as ‘the hat’the tile demonstrated aperiodic (irregular) tiling, unlike soft cells.
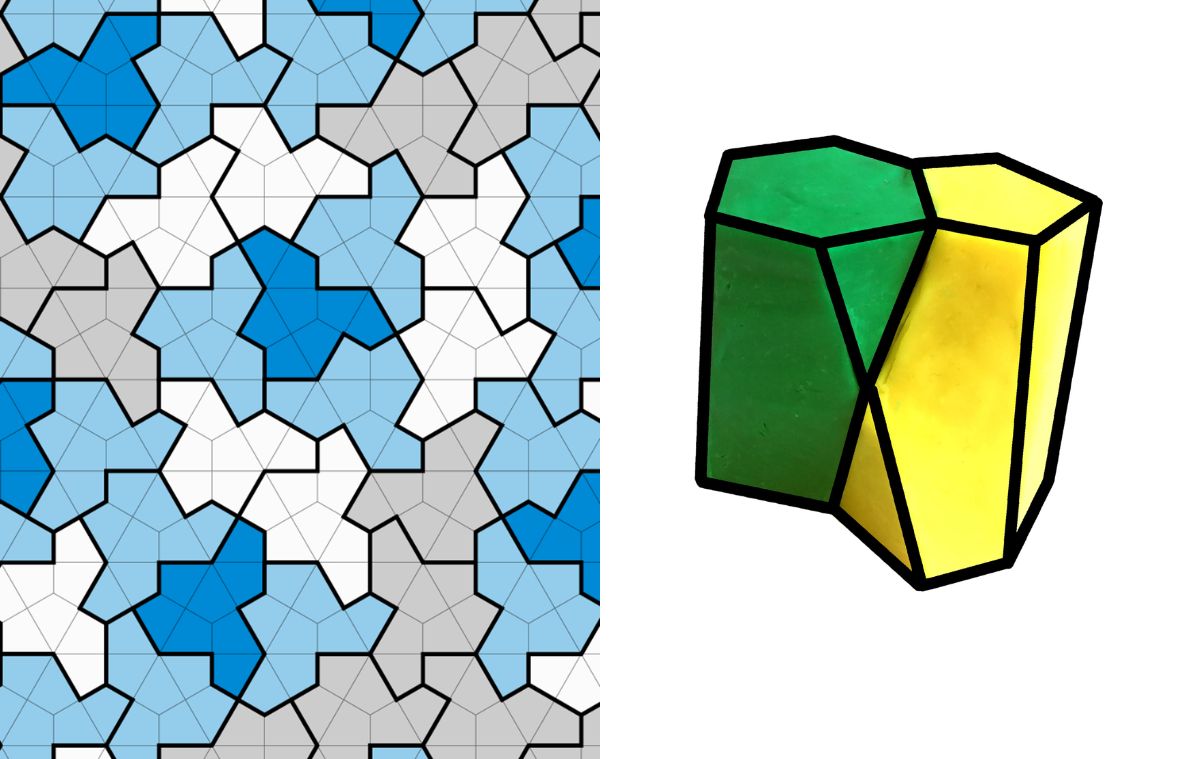Einstein tiles showing a non-repeating pattern; and (right) example of a scutoid.
Other shapes that have been discovered in recent memory are a ‘reinvented wheel’ that looks like a ‘multi-dimensional guitar pick’, and the scutoid. Spanish biologists had described the latter as a 3D shape adopted by our body’s epithelial cells in certain circumstances. Resembling a twisted prism, it allowed bodily tissue to curve, allowing our organs to shape properly during development.
Such discoveries allow creators to gaze upon new frontiers in art and math — two fields that seem distant, but have always been treated as unified by polymaths like Leonardo Da Vinci and Luca Pacioli. This approach best lends itself to inventions in everyday life, as puzzle designer Manish Rathod found out. You can read more about him twists on the classic Rubik’s Cube’s here.
For more alerts on logic and new ways of thinking, we invite you to explore @iepuzzles on Instagram.